Qui si parla di giochi/Games
In questa pagina metterò qualche pezzo su aspetti della teoria dei giochi. Uno è di una lunghezza micidiale, e in Inglese…ci sono anche cose più brevi
Un pezzo su Maddmaths
 L’idea del dilemma del prigioniero è maturata alla RAND corporation, una società di studi strategici fondata nel 1948. Gli ideatori della situazione, poi descritta dal dilemma, che però nella sua versione di storiella è stata formalizzata da A. Tucker nel 1950, furono Merrill Flood e Melvin Dresher.
L’idea del dilemma del prigioniero è maturata alla RAND corporation, una società di studi strategici fondata nel 1948. Gli ideatori della situazione, poi descritta dal dilemma, che però nella sua versione di storiella è stata formalizzata da A. Tucker nel 1950, furono Merrill Flood e Melvin Dresher.
Ecco il racconto della storiella:
Due tizi sono catturati dalla polizia perché fortemente sospettati di aver commesso un crimine. Il giudice, un giudice geniale, come vedremo, fa loro il discorso seguente:
So che siete responsabili della rapina di ieri. Per questo crimine la pena corrispondente è di 5 anni di galera. Se però uno confessa la partecipazione di entrambi al delitto, sarà libero per una legge sui pentiti, mentre l’irriducibile si prende delle aggravanti e sarà condannato a 7 anni di galera. Se nessuno dei due parla, dal momento che sono convinto che in un processo con giuria popolare sareste assolti, vi sanziono per una pena minore, cioé un anno di galera, per varie infrazioni gravi al codice della strada, senza portarvi a processo.
Come nella più ovvia tradizione matematica, riassumiamo, riportando gli anni di galera, nelle varie situazioni:
| 1\2 | Confessa | Non confessa |
| Confessa | 5;5 | 0;7 |
| Non confessa | 7;0 | 1;1 |
Che faranno i due, se si comportano razionalmente, e se quel che conta per loro sono gli anni di galera? La conclusione inesorabile è che entrambi confesseranno, e si faranno 5 anni di galera, pur avendo a disposizione una scelta congiunta, non confessare, che li farebbe avere solo un anno di galera. Una pausa prima di spiegare il perché di questa conclusione.
Ecco una frase presa dalla descrizione del dilemma da parte di Wikipedia, versione italiana.
Gli investigatori li arrestano entrambi e li chiudono in due celle diverse, impedendo loro di comunicare.
Ed ecco la versione Inglese
Each prisoner is in solitary confinement with no means of communicating with the other.
Se interrogate esperti o quasi esperti (tipo economisti, gente che la teoria dei giochi la mastica un po’), il 90% vi dirà la stessa cosa. Se poi uno è raffinato, vi dice pure che è un gioco a mosse contemporanee, e che se uno dovesse parlare per primo, la situazione cambierebbe.
Mi spiace, ma sono proprio sciocchezze. E non parlatemi male di Wikipedia, di solito molto affidabile (almeno, per la matematica). Ora spiego perché, e si vedrà che è facilissimo capire, ma tant’è uno dice per qualche motivo una cosa una volta, e poi le leggende sono difficili da estirpare…
Supponiamo per un secondo che uno debba decidere da solo (qui non si parla più di prigionieri, sto generalizzando…), che abbia dei costi da sostenere, e delle scelte da fare. Che fa secondo voi, da un punto di vista matematico, e non solo? Non è difficile direi, cerca di minimizzare I costi. Chiamata c la funzione costo, definita su qualche insieme di scelte X, e si studia il problema
c(x).
C’è bisogno di altre spiegazioni? Direi di no! Occorre affannarsi a spiegare regole per convincerci che quella è la cosa giusta da fare? No!, si parla di costi, che quindi vanno minimizzati e chiuso il discorso: provate voi a fare una teoria dell’ottimizzazione in cui la funzione costo non è minimizzata!
Ora, qual è la complicazione che la teoria dei giochi introduce? Di fatto, la presenza di un altro implica che in genere la funzione costo di un individuo dipende anche dalle scelte dell’altro individuo:
c=c(x,y).
Adesso che cosa voglia dire minimizzare in questo caso non è mica chiaro, visto che un agente ha la possibilità di scegliere una sola delle variabili in ngioco. Però supponete che succeda un caso incredibilmente fortunato:
Esiste x tale che
c(x,y)<c(z,y) per ogni z in X diverso da x, e per ogni y.
Insomma, esiste un elemento che minimizza i miei costi sempre, a prescindere da quel che fa l’altra persona!
Bene, questa è una situazione veramente estrema, direte che non succederà quasi mai, ed è vero: è banale rendersi conto che in genere una nostra scelta sarà buona o cattiva a secondo delle scelte dell’altro!
Però questa situazione “ideale” è proprio ciò che accade nel Dilemma del prigioniero, perché scegliere di confessare è SEMPRE più conveniente, qualunque cosa faccia l’altro!
E dunque non occorre affatto tenere separati questi prigionieri, non occorre affatto supporre che il gioco sia a mosse contemporanee, è ridicolo sostenere che se uno parla per primo la situazione cambia…tanto ognuno di loro sa che farà l’altro, e quindi giocare prima o dopo, parlare o no, non cambia proprio nulla.
Perché questi errori? Forse, in parte perché in un equilibrio di Nash in effetti la situazione non è così chiara come qui, dove si parla di strategia fortemente dominante. In una situazione di equilibri di Nash, se uno parla per primo può indirizzare le scelte…ma qui la situazione è ben diversa.
Il primo che avuto l’idea peregrina di dire che i prigionieri vadano tenuti separati voleva forse in qualche modo sottolineare che occorre evitare, per esempio, che i due possano minacciarsi, cioè dirsi cose tipo “se parli faccio ammazzare qualche tuo parente”. Però mi pare evidente che così si sta cambiando il gioco…cioè si sta cambiando le funzioni costo dei giocatori, e allora si deve semplicemente studiare un’altra tabella di costi, non dire che per ottenere la soluzione giusta per la tabella di sopra devo specificare procedure stravaganti… Questo però è un discorso che non è tanto facile da accettare, forse perché mostra come i matematici abbiano una marcia in più, quando si tratta di fare modelli…dico questo, perché ho parlato del Dilemma con uno psicologo di grande reputazione, che voleva mostrarmi che i matematici sbagliano a postulare che le persone perseguano la massimizzazione dell’utilità. E per convincermi di questo mi ha fatto leggere una ricerca di alcuni colleghi, pubblicato in una rivista importante, in cui gli autori volevano appunto confutare l’idea che l’agente massimizzi la propria utilità. Per fare ciò, hanno ideato un esperimento tipo Dilemma del prigioniero, che in questo caso potrebbe essere esemplificato con la formula “vuoi che dia 10 Euro a te o 100 al tuo collega?”. Ancora una volta la corretta risposta razionale, dammi 10 Euro, va a scapito di una situazione più favorevole per entrambi (ma insostenibile, in assenza di vincoli). Nella prima fase dell’esperimento, dicevano all’intervistato che l’altro aveva già manifestato l’intenzione di chiedere i 10 Euro per sé. E il 98% delle persone a sua volta chiedeva i 10 Euro. Nella seconda fase, gli sperimentatori provavano a convincere che l’altro lo aveva fatto perché costretto, e che era in difficoltà economiche, che forse meritava un gesto di simpatia e, voilà, un buon numero di loro cambiava opinione e accettava l’idea di dare i 100 Euro all’altro, andando quindi contro il principio della massimizzazione della propria utilità… proprio no!
Il Dilemma è stupendo anche perché ci mostra quanto sia facile equivocare, se non si è matematici…l’esperimento non ha mostrato che si sbagliano i matematici, ha mostrato che gli psicologi non hanno capito che cosa hanno fatto nell’esperimento: inducendo empatia verso l’altro, hanno semplicemente cambiato la funzione di utilità di molti intervistati, che continuano a fare una scelta coerente, però secondo parametri diversi.
Anche se i giornali raccontano solo cose truci, ogni giornata è piena di gesti di gratuita generosità da parte di tante persone. Non sono persone irrazionali, non sono persone che non sanno massimizzare la loro utilità, sono semplicemente belle persone, che massimizzano la loro soddisfazione personale, per esempio, facendo un gesto che apparentemente, ma solo apparentemente, non porta loro un guadagno tangibile.
Un altro pezzo scritto tempo fa per Maddmaths (credo!)
 Datemi due ore di tempo e io vi parlerò del concetto di strategia mista.
Datemi due ore di tempo e io vi parlerò del concetto di strategia mista.
Pensate che sia uno scherzo di carnevale? Proprio no, ne fa fede il fatto che i giochi sono la cosa più seria che ci sia, quindi occuparsi di giochi è importante e rende molto autorevoli, e analizzare i giochi senza il concetto di strategia mista è proprio impossibile. La locuzione “strategia mista” contiene due parole, quindi per cominciare prendiamoci il tempo adeguato per capire prima di tutto che cosa è una strategia; il mista seguirà. Dato un gioco qualunque, si chiama strategia per il giocatore una specificazione di ciò che fa in ogni situazione possibile in cui è chiamato a prendere una decisione. Per fare un esempio pensiamo al gioco del tris, nel quale si tratta di scegliere a turno un quadratino tra nove, mettendoci il proprio simbolo, con lo scopo di cercare di fare una riga di propri simboli, in orizzontale, verticale o in diagonale, e tutti capiscono la mia spiegazione, perché tutti ci hanno giocato almeno una volta, durante certe ore di noia mortale passate a scuola.
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
Proviamo allora a immaginare di scrivere una strategia del primo giocatore, Alberto, che gioca contro Bob, e che mette X nella casella scelta, mentre Bob usa una Y:
- Metto X nella casella numero 1
- Se Bob mette Y nella 2 allora io metto X nella 3, se Bob mette Y nella 3, allora io metto X nella 4,… se Bob mette Y nella 9 allora metto X nella 2
- Se la situazione attuale è 1 (X) 2(Y) 3(X) 4(Y) allora metto X nella 5, se è 1 (X) 2(Y) 3(X) 5(Y) allora metto X nella 4, se…
- …
- …
Insomma, mica una cosa semplice. Però è chiaro che, con questa definizione, quando i due giocatori specificano una strategia ciascuno, si sa che partita è effettivamente (e si potrebbe pure notare che le informazioni fornite dalle strategie sono persino ridondanti). Comunque, la cosa importante è che la definizione di strategia ci permette di dire che quando i giocatori ne annunciano una ciascuno, l’esito del gioco è determinato.
A che ci serve tutto questo? Come ogni cosa che si fa in matematica, ci deve servire per ottenere informazioni. In questo caso, sul comportamento di giocatori razionali. E nell’esempio precedente tutti o quasi sappiamo che il risultato non può essere diverso dal pareggio: due che sanno analizzare le cose devono concordare che il risultato inevitabile è il pareggio… e se non siete convinti, pensate a un gioco molto stupido: ci sono 4 carte sul tavolo, ogni giocatore ne deve togliere una o due, e chi toglie l’ultima perde. E’ evidente che vince il secondo: se al primo turno il primo ne toglie una, lei ne toglie due lasciando il primo con una carta sul tavolo, se ne ha tolto due, lei ne toglie una…quindi tra due giocatori capaci di fare l’analisi del gioco al livello di profondità necessaria l’esito del gioco è sempre lo stesso.
Tutto questo succede nei giochi a informazione perfetta, cioè in quei giochi in cui tutto è noto ai giocatori, in ogni istante di ogni possibile partita. Come ad esempio la dama, gli scacchi, o il go, per citarne tra i più famosi.
Bene, un importante teorema afferma che in questi giochi i giocatori hanno strategie di gioco ottimali, quindi un esito prevedibile, purché i giocatori abbiano il livello di razionalità adeguato.
Tuttavia, non tutti i giochi ricadono nella categoria di quelli a informazione perfetta. Se gioco a carta, sasso forbici, io non conosco la mossa del mio avversario (infatti nessuno accetta di giocare per primo a questo gioco se la mossa del primo è visibile). E per fortuna nessun teorema ci garantisce che l’esito di questa partita tra due giocatori razionali è scontato: mettete pure a giocare Gödel e Turing, ma chi vince una singola partita non potete prevederlo, e nemmeno prevedere il pareggio. E quindi non ha senso parlare di strategie ottimali in questo caso, cioè strategie che un giocatore sceglie sempre quando gioca, perché di meglio non potrebbe ottenere. Infatti se qualcuno vi osserva giocare a carta sasso e forbici parecchie volte in una stanza, anche con giocatori diversi, si stupirebbe, se vi ritiene intelligente, di vedervi giocare sempre la stessa cosa, ad esempio sasso.
Ecco che comincia a insinuarsi l’idea di mischiare un po’ le carte.
Una strategia mista è dunque una distribuzione di probabilità sulle strategie pure. Nel nostro esempio, potrei decidere di giocare il 50% delle volte carta e il 25% per cento le altre due (25% ciascuna, altrimenti…). Ma sarebbe una buona idea? Certo, meglio che giocare sempre carta (cioè una strategia pura): uno che mi osserva dopo un po’ capisce, e con me vincerà sempre. Ma anche la strategia di sopra non è ottimale, perché il secondo giocando sempre forbici si garantisce, alla lunga, di guadagnare qualcosa, il che non è logico in un gioco simmetrico.
Un meraviglioso teorema ci garantisce che nei giochi competitivi (in breve, quelli dove se io guadagno qualcosa il mio avversario perde la stessa cosa) esiste sempre un modo ottimale di giocare per i giocatori. Il che significa che, in media, il risultato è prevedibile!
Non potevamo pretendere di più. Ma dai matematici un teorema del genere ce lo possiamo aspettare perché, se non possiamo arrivare a un risultato, possiamo accontentarci di risultati parziali significativi: se un problema è impossibile da risolvere, provo a trovare qualcosa di meno della soluzione classica del problema, ma pur sempre significativo.
Astrazioni da matematici? Forse, ma astrazioni molto realistiche. Perché la vita, quando non è proprio gioco, è almeno modellizzabile come gioco, e di solito il gioco non è a informazione perfetta: proprio per questo usiamo sempre o quasi strategie miste.
Insomma, nonostante quel che pensava Einstein, forse Dio ha giocato davvero a dadi, e certamente costringe noi a giocare ai dadi: sta a noi farlo in maniera intelligente, scegliendo la strategia mista più appropriata.
 Game theory: a user’s guide (from my own point of view, of course)
Game theory: a user’s guide (from my own point of view, of course)
Life exists because there is interaction. Every living being is in contact and interacts with external reality throughout its life cycle, often in a totally unconscious way from the intellectual viewpoint, sometimes aware of the consequences of its actions. The mathematical theory that deals with interactions is commonly known by the very effective name of game theory: effective, in particular, because game is a beautiful model of interaction. Game theory has applications in every field and is also a very valuable test to measure the effectiveness of many methods for solving complex problems. The reason is very simple. A game often has clear, easy to understand rules, but then it is terribly difficult to analyse: even in an advanced course in game theory, if students do not have specific software, they can only perform calculations for absolutely trivial games, and even then such calculations may not be too simple. For instance, calculating mixed strategies for a two-player game where each player has three available strategies is a long and tedious process, despite the enormously limited number of actions available to the players (and if you look at Appendix 1, you’ll find an interesting story about the game of draughts, or checkers). Beyond this aspect, there is an extremely important question that we have to ask ourselves about this theory, which after all has very recent origins: how reliable is such a mathematical theory?
This is an important question because, while we are all aware that mathematics obviously introduces many simplifications in its models, at least in not particularly sophisticated theories we are also used to the fact that these simplifications, if the models are well made, do not lead to unpredictable and perhaps devastating results. Errors of approximation and simplification do not preclude great results; the model that carries a space probe around the universe probably includes several approximations, to make the problem tractable, but then, at the end of the day, the results are obtained. What happens in game theory?
We are talking about a theory that, at least at its beginnings, had above all the ambition of describing scientifically the behaviour of the rational man. Now, we see right away that even to start is difficult, because it is a matter of giving a definition, even if not necessarily a formal one, of the concept of rationality. But this is just the first, tiny step. A next, much harder one immediately awaits us: once we have this definition, or at least an idea of it, how far can the results so obtained be applied to the real world? In other words: when we make people “play”, do they behave in the way prescribed by theory or not, are they rational or not? At least when experimenting with simple games, you might think that making the appropriate verifications is not difficult… but this is not so.
Let us perform, or better imagine, a quick experiment. We take two people and say, publicly, to each of them: “Do you prefer me to give 1 euro to you, or 20 euros to the other player”? Now we can observe different possibilities: for instance, both could say, “Give me 1 euro”, or to the contrary, both could say “Give 20 euros to the other player”. It is obviously not even impossible to imagine the case in which one says, “I want 1 euro for me” and the other, “Please give 20 euro to the other player”. The theory, presumably, suggests what the rational outcome of a game like this is and therefore, if one outcome is the correct one, the other ones are necessarily wrong! Unfortunately, or perhaps fortunately, it is not so simple.
How can an answer be rational, when theory signals it as wrong? The subtle and complicated issue is to be sure of what the players’ goals really are, when confronted with a game like the one we have just described. In other words, what do the two players actually want? The theory quite naturally assumes that, for every player, having more, in monetary terms, is always better than having less. But can I be sure that those who say, “Give 20 euros to the other person” are doing something irrational? To be sure of the conclusions I have obtained through the theory, I need to be sure of how the players evaluate different situations.
In a game like this, which is apparently so simple but actually so interesting and challenging (it is a variant of the most famous of all the examples in game theory, the prisoner’s dilemma), there are also other factors that can affect the responses of rational players. For instance, if they are intimately convinced, even unconsciously, that the game will be played repeatedly, then answers that are not rational in the game played only once can become so if the game is repeated.
Another famous and interesting example goes by the name of “ultimatum game” and can be briefly described as follows: the first player is told that there are 100 euros available and that he must offer a part x of them, x ≥ 1, to the second player: if the latter accepts, x will be given to the second and the remainder to the first, while if the second player does not accept neither one gets anything.
This game was tested on people (paid to play), who had to accept or reject the offer x and on whom, during the game, a brain MRI scan was being performed, to see which areas in the brain were being activated. Again, if having more money is better than having less money, even an offer of x = 1 should be accepted. Yet this does not happen in practice, and perhaps it is no coincidence that when the second player was told that the offer was generated by a computer, then the average accepted bids dropped significantly. What determines the rejection of an x that is deemed too low? Apparently, entering into the evaluation a person makes are other factors which are much more imponderable than the mere economic evaluation and make it very arbitrary to conclude that the player behaves irrationally.
To sum up all of this, and neglecting other aspects, though important, I often like to say that it is one thing to predict the movements of Jupiter, meant as a planet, and another to make predictions about Jupiter, meant as the god of the Romans: we cannot expect equally reliable results in both cases.
A truly crucial question then arises spontaneously: how useful is this mathematics whose reliability is not clear? The question is pretty important and concerns more than just game theory, because other human disciplines have recently started using mathematics in a massive way; just think of the theory of social choices or economy, not to mention medicine and psychology. So, how reliable are these theories?
Game theory – this is my opinion – it is not a mathematics that is beautiful but has limited practical utility. On the contrary, it is a powerful tool, but it must be used with extreme critical sense. I would be horrified if in some international crisis decisions were made on the basis of pre-packaged models by experts in game theory: the situations at stake are always very complex and have specific aspects that make them unique; it is easy to get some uncertain parameter of the problem wrong and to obtain answers that could in retrospect prove to be disastrous.
But there are also far more usual situations, where such answers might be acceptable. If I have to establish how to allocate certain expenses for the construction of a so-called common good, using the Shapley value is an excellent idea. Furthermore, there are situations in which a game theory expert can certainly help people to make sensible decisions, for example, in the case of a company wanting to participate in an important auction. Let me stress help, since no one can guarantee winning an auction. I myself was approached by a company that asked me if I was willing to help them in a similar situation – and we can very well discuss such a collaboration – arriving inevitably to “Then, with your advice, are we sure to we win the auction?” At that point, my answer was that, as far as I knew, the ten richest men in the world were not experts in game theory, and the thing was over.
But there is another point. This theory is not only of avail, if used judiciously, in some specific situations. By teaching game theory, by talking about it on many occasions, in short, by continuing to reflect about it, I came to the conclusion that this mathematics has an inestimable value, less practical than problem-solving, but certainly not less valuable: it leads those who know it to seeing things in a different way than usual, and this different way can be really precious.
Here are a couple of illuminating examples.
When a rational decision maker is faced with alternatives, having many possible choices is obviously a good thing. If I need to buy a pair of shoes and go into a shop which I usually patronise, discovering that it has acquired an extra room so that in addition to the shoes I usually find there, there are more of different brands, is a pleasant surprise: I have more possible choices, so in the end I will be more satisfied (I’m talking about rational players). Mathematically, I’m saying a very trivial thing: given a function u that represents the utility that I associate with each type of shoes, and given two sets A and B, which represent the sets of shoes out of which I can choose my pair, then if B ⊃ A, the maximum of u on B is certainly not less than that on A, which means that I shall not go out of the shop less happy when I have more choices.
Let us now consider a group of rational decision-makers. Will the same thing happen? Our intuition, I think, is that if they are rational, they will still be able to choose the right alternatives: how could a greater possibility of choice lead to worse results?
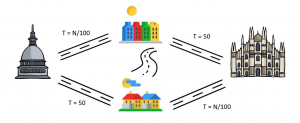
Let’s look at an interesting example, which deals with the traffic problem exemplified in the figure below.
Every morning at 7 a.m. a given number of people must go from Turin to Milan and have two alternative ways through two intermediate towns, one more to the north and one more to the south. Both routes consist of an urban section, in which travel time depends on the traffic there, and lasts N/100 minutes, where N is the number of cars that are on the road, and a highway, where the travel time is fixed, 50 minutes, because it is regulated by speed limit enforcement. Suppose now that there are 4000 people travelling, each in a car. How long will they take to go from Turin to Milan? There is no need to know what a Nash equilibrium is to convince oneself that what will happen is that, given the perfect symmetry of the two routes, one half of motorists will take the northern route, the other half the southern one, with the result that each will take 20 + 50 = 70 minutes for the trip.
Suppose now that the efficient mayors of the two towns, which are very close, decide to build a very wide road to connect them, so it is possible to get from one town to the other one in five minutes. What happens now? Any rational driver would realise that if he took the highway to the southern town, the trip would take 50 minutes, while if he passes through the northern town first, it would take at the most 45 minutes to arrive to the southern town. Thus, for him the only rational action would be to move through North. Of course, everyone would reason like this, so in the end everybody’s travel time would become 85 minutes!
What happened? It is no coincidence that this example takes the name of Braess’s paradox: the paradox lies in the difficulty our mind has in accepting that in interactive situations, albeit with rational agents, there may exist alternatives that eventually lead to negative results for everyone: the mayors must weigh accurately the pros and cons before building a new road!
Here is an important first lesson from the theory: giving players more choices may be detrimental to them, even if they are smart players!
There is another example, which I consider wonderful, of an unorthodox reflection that a game theorist can do and try to explain. The details are given in Appendix 2; here I say only that it is the notion of correlated equilibrium: the players, which as we know are supposed to be selfish and rational, decide to agree on a probability distribution of the outcome of the game (this makes sense when there are no pure equilibria or they are not very interesting). Then they enact a random mechanism that selects an outcome. Finally, there is a mediator, possibly a suitably programmed computer, which, based on the outcome selected by the random event, tells each player what they should do. If the probability distribution is chosen wisely, the players have no interest in deviating from the received recommendation (whatever this recommendation was), and in addition they get a higher utility than the Nash equilibrium! Where is the beauty of the message that this idea brings? There are at least two extraordinary aspects: first, even in a selfish world a limited, rational collaboration that is beneficial for all may be possible; second, this collaboration is possible only under certain conditions. In this case, the players have to give up some information: the mechanism only works because each player is told only what he is to do but not what the others are told. But this is important: the choice of the players is a conscious one, they are the ones who choose the probability distribution on the outcomes, they are the ones who accept the mechanism.
To conclude, then, a lucid analysis of the situation, even starting from the (very reasonable) assumption that people basically act in their own interests, shows that it is possible to create the bases of a collaboration that can bring benefits to everyone.
Appendix 1. A game or a test?
“Checkers is solved” is the title of a paper published in Science in 2007 [Sch]. Someone computed that in the game of draughts there is an approximate number of 5×1020 possible positions. It is clear that such a game cannot be analysed in its entirety. Yet, we know that rational players would always get the same result. In technical terms, we say that the game has an equilibrium in pure strategies and it is also known that in the case of multiple equilibria (which the theorem does not exclude a priori) the result would still be the same: this depends on the fact that it is a zero-sum game, assuming to award +1 to the winner, –1 to the loser and zero for a draw. But then the question becomes: which of the three possible results is the actual one? That paper shows that the correct result is a draw, just as in noughts and crosses (tic-tac-toe), two rational players would always get a draw. How was this result proved? The proof is really a product of our times, because it uses a mixed technique: the problem is simplified mathematically, then is tackled with powerful computing algorithms, based in turn on typical methods of game theory, in particular the method of backward induction, which however can be applied to very simplified situations (for instance, a chessboard with a very limited number of pieces on it). The work is the result of at least 20 years of work: the game has been a formidable test to make the tools of artificial intelligence increasingly sophisticated.
Appendix 2. Correlated equilibrium
Consider the game described by the following table:
| Left | Right | ||
| High | (7, 2) | (0, 0) | |
| Low | (6, 6) | (2, 7) | |
There are two players, each with two strategies. For the sake of simplicity, let us say that the first player can choose between High and Low and the second between Right and Left. This game has three Nash equilibria: two in pure strategies and one in mixed strategies. The equilibria in pure strategies consists in playing High, Left and having as utility (7,2), or playing Low, Right with utility (2,7). The equilibrium in mixed strategies is instead given by the strategy (1/3, 2/3) played by the first player and (2/3, 1/3) by the second one. In this case, the expected utility for both players is 14/3. In some ways this balance is the most interesting, as it yields the same utility to both players; moreover, as we can see by looking at the table, the two players are in a symmetrical situation and, out of a sense of justice, the equilibria in which the result is the same for both seem better. If the equilibrium in mixed strategies is played, the probability distribution on the outcomes of the game is as follows:
| 2/9 | 1/9 |
| 4/9 | 2/9 |
That is, with probability 2/9 “High, Left” or “Low, Right” will be played, which correspond to the results (7, 2) and (2, 7); with probability 1/9 the two players will choose “High, Right”, with outcome (0, 0), and with probability 4/9 they will play “Low, Left” with result (6, 6).
Let’s then try to change the probability distribution on the outcomes. Consider, for instance, this probability distribution:
| 1/3 | 0 |
| 1/3 | 1/3 |
where each non-zero outcome is played with equal probability. With this probability distribution the players would end up better than with the equilibrium in mixed strategies, because now they would get 15/3 rather than 14/3!
But how could we convince them to accept that kind of probability, since it is not a situation of Nash equilibrium? The idea is to invent a mechanism, the following: we agree that a die is cast by a third person, who observes the outcome and then suggests privately to each player what they should do. This private information forces rational players to update their odds on the outcomes (for instance, if the player who chooses the row is told to play the second row he knows that the outcome “Low, Left” and “Low, Right” have the same probability). With this update, the player who chooses the row now asks themselves: is it then better for me to deviate from the recommendation or not? With simple calculations, it turns out that for the players it is not convenient to deviate, whatever the suggestion they received privately. This is the brilliant idea of correlated equilibrium.
Translated from the Italian by Daniele A. Gewurz
References
[Ber] Bernardi, G., Lucchetti, R.: È tutto un gioco. Introduzione ai giochi non cooperativi. Francesco Brioschi, Milan (2018)
[Sch] Schaeffer, J. et al.: Checkers is solved. Science 317, 1518–1522 (2007)